What are p-adic numbers ?

P-adic and rationnal numbers

P-adic numbers are an original way to look at the (limit of sequence of) elements in \(\mathbb{Z}\).

More precisely, just like \(\mathbb{R}\) represents the limits of Cauchy sequences in \(\mathbb{Q}\) endowed with the distance : \(d(x,y)=x-y\), \(\mathbb{Z}_{p}\) represents the limits of Cauchy sequences in \(\mathbb{Z}\) with another distance : \(d_p(x, y)\), where \(d_p\) is detailed below.

P-adic valuations

For \(p\) a prime number, define \(\mathrm{ord}_p(a)\) as the exponent of \(p\) in the decomposition of \(a\) in a product of prime factors. Also define \(\mathrm{ord}_p(0)=\infty\)

Then \(d_p(a,b)=p^{-\mathrm{ord}_p(a-b)}\) is a distance on integers.

In \(\mathbb{Z}\) with the distance \(d_3\), note that the sequence \((3^n)_n\) converges towards \(0\).

Why they matter

Various results can be proved using p-adic numbers. I discovered them in “Introduction to number theory”, where they are used to determine whether an ellipse has rationnal points. They also enable to give a meaning to \(\sum 5^i = -\frac{1}{4}\)

Visualization

The idea

A p-adic number can be written \(\sum_{i} p^i a_i\) where the sum might be infinite. Though it seems weird because the terms are growing, note that the sequence \((p^i)_i\) actually tends to \(0\) really quickly in \(\mathbb{Z}_{p}\)

A traditionnal way to picture p-adic numbers is with co-centric circles, like below:

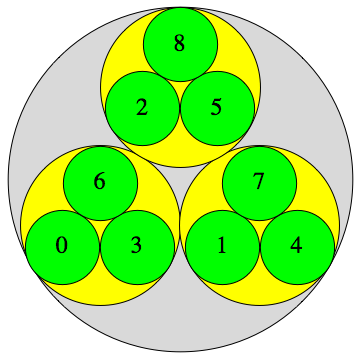
All the credit goes to: Heiko Knopse for this illustration, more are available on his site

My idea is to take this idea to the limit. Formally, for \(n=\sum_{i} p^i a_i\), the complex number \(z=\sum_{i} l^i \exp \left( a_i \frac{2i\pi}{p} \right)\) is associated to \(n\).

\(l\) is a parameter between \(0\) and \(1\) used to ensure convergence.

Results

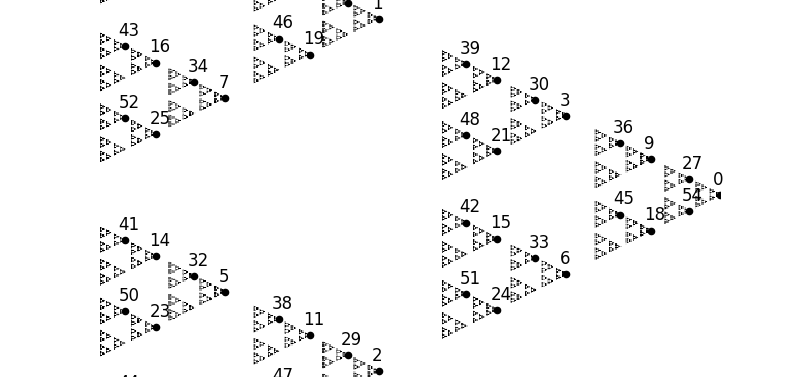
Representing some integers

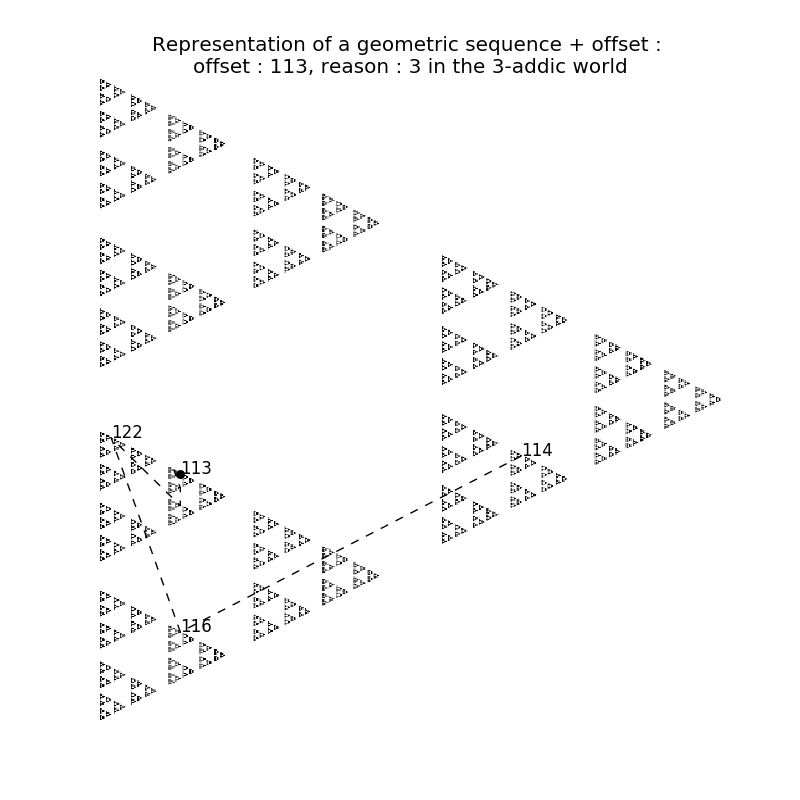
Convergence

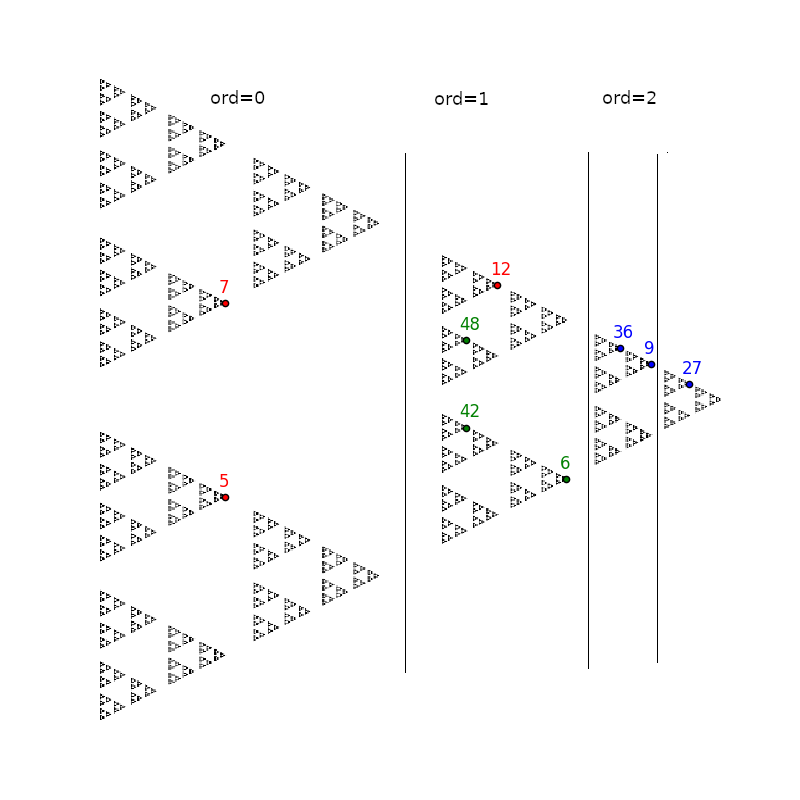
Addition

An interesting property is that \(\mathrm{ord}_p(a+b) \geq \min(\mathrm{ord}_p(a), \mathrm{ord}_p(b))\). It is illustrated below. As you can see, addition in the p-addic representation shifts numbers to the right.

Learning more

For those interested in number theory, I strongly recommend the following books, they are the reason I discovered p-adic integers and they motivated me to explore them (and write this article!)

Number Theory 1: Fermat’s Dream by Kazuya Kato, Nobushige Kurokawa and Takeshi Saito

Number Theory 2: Introduction to Class Field Theory by the same authors which requires more knowledge in algebra and group theory.

“One square and an odd number of triangles”, a problem from Proofs from the book also makes an amazing use of p-adic valuations. The problem itself is simple to state:

is it possible to dissect a square into an odd number \(n\) of triangles of equal area?

And this concept appears here, quite surprisingly.

Code

from cmath import *


class PAddicRepresenter:

    def __init__(self, p, l, output_length=30):
        self._p = p
        self._l = l
        self._output_length = output_length

    def to_plane(self, n):
        l = self._l
        p = self._p
        decomposed_int = self._completed_int_to_base(n)
        complex_coordinates = sum(
            [l ** n * exp(1j * c * 2 * pi / p) for n, c in enumerate(decomposed_int)])
        return complex_coordinates.real, complex_coordinates.imag

    def transform_sample(self, ns):
        xs, ys = [], []

        for n in ns:
            x, y = self.to_plane(n)
            xs.append(x)
            ys.append(y)

        return xs, ys

    def _int_to_base(self, n):
        p = self._p
        i = 0
        decomposition = []
        while n > 0:
            residual = n % p
            n = (n - residual) / p
            decomposition.append(residual)
        return decomposition

    def _completed_int_to_base(self, n):
        decomposed_int = self._int_to_base(n)
        return decomposed_int + [0] * (self._output_length - len(decomposed_int))

The first visualization being obtaining using the following:

import matplotlib.pyplot as plt
plt.rcParams["figure.figsize"] = (8,8)
from PAddicRepresenter import PAddicRepresenter


n_points = 3**10
p = 3
small_sample_size = 55
l = 0.45

par = PAddicRepresenter(p, l)

xs, ys = par.transform_sample(range(n_points))

fig, ax = plt.subplots()

ax.hist2d(xs, ys, bins = 500, cmap = 'Greys')

ax.scatter(xs[0:small_sample_size], ys[0:small_sample_size], c='black')
for i in range(small_sample_size):
    ax.annotate(str(i), (xs[i] - 0.03 , ys[i] + 0.05))
 
plt.axis('off')
plt.show()