At the heart of our AI lies the powerful Min-Max strategy, a method that has revolutionized the way machines approach decision-making in two-player games. With OCaml’s elegance and expressiveness, we delve into the intricacies of this strategy, exploring how it enables our AI to not just play, but dominate, the age-old game of Tic-Tac-Toe. Whether you’re a seasoned programmer, a curious AI enthusiast, or simply a Tic-Tac-Toe aficionado, this article promises to shed light on the inner workings of AI-driven game strategy and the wonders that OCaml brings to the table. So, let’s embark on this exciting journey and unlock the secrets behind a Tic-Tac-Toe AI that can never be beaten.
Let’s start with the definition of the pieces:
type piece = Cross | Circle
let piece_opposite = function
| Cross -> Circle
| Circle -> Cross
let add_color color s = "\027[3" ^ color ^ "m" ^ s ^ "\027[39m"
let piece_option_to_string = function
| Some(Cross) -> add_color "1" "X"
| Some(Circle) -> add_color "6" "0"
| None -> " "
We will represent the board as a piece option array array. The option is None if the board is empty at a specific position, otherwise, it is Some(piece)
We also want to render the board so that a human can easily play :)
type board = piece option array array
let board_at board i j = board.(i).(j)
let board_init _ =
Array.init 3 (fun _ -> Array.make 3 None)
let board_copy b =
let res = board_init () in
let n,p = 3, 3 in
for i = 0 to n - 1 do
for j = 0 to p - 1 do
res.(i).(j) <- b.(i).(j)
done
done ;
res
let board_place board piece i j =
let board' = board_copy board in
let () = board'.(i).(j) <- Some(piece) in
board'
let board_transpose b =
let res = board_init () in
let n,p = 3, 3 in
for i = 0 to n - 1 do
for j = 0 to p - 1 do
res.(j).(i) <- b.(i).(j)
done
done ;
res
let board_print b =
let print_separator () =
print_string "+" ;
Array.iter (fun _ -> print_string "-") b.(0) ;
print_string "+\n"
in
let print_row r =
print_string "|" ;
Array.map piece_option_to_string r |> Array.fold_left ( ^ ) "" |> print_string ;
print_string "|\n"
in
print_separator () ;
Array.iter print_row b ;
print_separator ()
So, we only have pieces and boards so far, time for some game logic.
let has_won piece board =
let winning_line = Array.for_all (fun x -> x = Some(piece)) in
let is_main_diagonal_winning = Array.for_all (fun x -> x = Some(piece)) [| board.(0).(0); board.(1).(1); board.(2).(2) |] in
let is_other_diagonal_winning = Array.for_all (fun x -> x = Some(piece)) [| board.(0).(2); board.(1).(1); board.(2).(0) |] in
Array.exists winning_line board
|| Array.exists winning_line (board_transpose board)
|| is_main_diagonal_winning
|| is_other_diagonal_winning
let has_lost piece board =
has_won (piece_opposite piece) board
let winning_board_cross = [|
[|Some(Cross); None; None|];
[|Some(Cross); Some(Circle); None|];
[|Some(Cross); Some(Circle); None|];
|]
let winning_board_circle = [|
[|Some(Cross); None; Some(Circle)|];
[|Some(Cross); Some(Circle); None|];
[|Some(Circle); Some(Circle); None|];
|]
let empty_board = board_init ()
let () = assert (has_won Cross winning_board_cross)
let () = assert (has_won Circle winning_board_circle)
let () = assert (has_lost Circle winning_board_cross)
let () = assert (has_lost Cross winning_board_circle)
let () = assert (not (has_lost Cross empty_board) && not (has_lost Circle empty_board))
let () = assert (not (has_won Cross empty_board) && not (has_won Circle empty_board))
let possible_moves board =
let all_moves = List.init 3 (fun i -> List.init 3 (fun j -> (i,j))) |> List.flatten in
List.filter (fun p -> board_at board (fst p) (snd p) |> Option.is_none) all_moves
let _ = assert (List.length (possible_moves winning_board_cross) = 4)
let is_game_over board =
has_won Cross board
|| has_won Circle board
|| Array.for_all (Array.for_all Option.is_some) board
let () = assert (is_game_over winning_board_cross)
let () = assert (is_game_over winning_board_circle)
The evaluation function is a critical component of an AI-powered Tic-Tac-Toe player utilizing the Min-Max strategy. Its primary role is to assess the current game state and assign a numerical value that reflects the desirability of that state for the AI player. This numerical value serves as a basis for the Min-Max algorithm to make informed decisions about which moves to choose during the game.
let eval player board =
if has_won player board then
1
else if has_lost player board then
~- 1
else
0
let () = assert ((eval Cross winning_board_cross) = 1)
let () = assert ((eval Circle winning_board_cross) = ~-1)
let () = assert ((eval Circle winning_board_circle) = 1)
let () = assert ((eval Cross winning_board_circle) = ~-1)
In the context of the Min-Max algorithm, the evaluation function often works in tandem with recursive calls. As the Min-Max algorithm explores possible future game states through a tree of possibilities, the evaluation function helps assess these states at different depths. The AI calculates scores for each state, and these scores are propagated up the tree to make informed decisions.
Let’s define a tree
type 'a tree =
| Node of 'a * 'a tree list
| Leaf
let tree_to_list tree =
let rec aux = function
| Leaf ->
[]
| Node (n, children) ->
n :: List.fold_left List.append [] (List.map aux children)
in
aux tree
And the tree of moves.
let make_moves_tree max_depth board player =
let rec aux depth board player =
let moves = possible_moves board in
match moves, depth with
| [], _ -> Node(board, [Leaf])
| _, 0 -> Node(board, [Leaf])
| l, d -> if (is_game_over board) then
Node(board, [Leaf])
else
Node(board,
List.map
(fun m -> aux (d - 1) (board_place board player (fst m) (snd m)) (piece_opposite player) )
moves)
in
aux max_depth board player
Now we are in a position to implement the evaluation function, taking into account future states. As the min max name suggests, we will need the following two functions:
let list_max l = List.fold_left Int.max Int.min_int l
let list_min l = List.fold_left Int.min Int.max_int l
let () = assert (list_min [1;3;2] = 1)
let () = assert (list_max [1;3;2] = 3)
And we are now in a position to have a full evaluation function!
let evaluate_board max_depth board player =
let tree = make_moves_tree max_depth board player in
let rec aux d tree = match tree with
| Node(b, [Leaf]) -> eval player b
| Node(b, l) ->
if (d mod 2 = 0) then list_max (List.map (aux (d+1)) l)
else list_min (List.map (aux (d+1)) l)
| Leaf -> failwith "Should not happen"
in aux 0 tree
let () = assert ((evaluate_board 1 winning_board_cross Cross) = 1)
let () = assert ((evaluate_board 1 winning_board_cross Circle) = ~-1)
Finding the best move is just a matter of minimizing the opponent evaluation function:
let find_best_move max_depth board player =
let moves = possible_moves board in
let possible_boards = List.map (fun m -> board_place board player (fst m) (snd m)) moves in
let scores = List.map (fun b -> evaluate_board max_depth b (piece_opposite player)) possible_boards in
let moves_and_scores = List.combine moves scores in
let best_move_and_score = List.sort (fun x y -> Int.compare (snd x) (snd y)) moves_and_scores
|> List.hd in
best_move_and_score |> fst
let almost_winning_board = [|
[|Some(Cross); None; None|];
[|Some(Cross); None; None|];
[|None; Some(Circle); Some(Circle)|];
|]
let () = assert ((find_best_move 2 almost_winning_board Circle) = (2,0))
let () = assert ((find_best_move 2 almost_winning_board Cross) = (2,0))
And the playing loop:
let max_depth = 9
let rec play board player =
let () = board_print board in
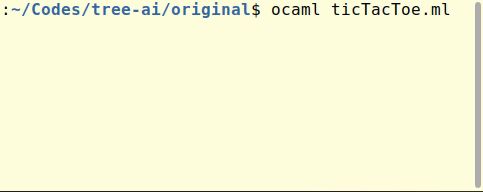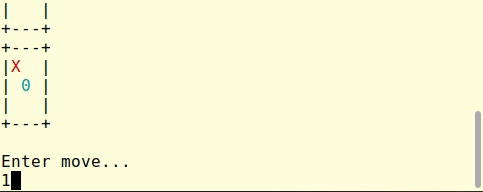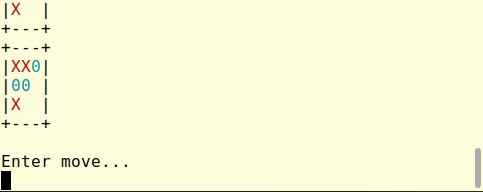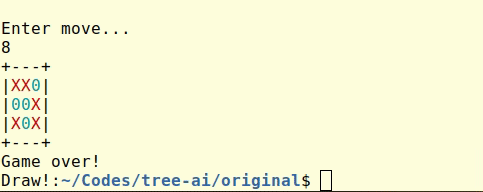
if (is_game_over board) then begin
print_string "Game over!\n" ;
if has_won Cross board then
print_string "You won!\n"
else if has_won Circle board then
print_string "Computer won!\n"
else
print_string "Draw!"
end
else
match player with
| Cross ->
let () = print_string "\nEnter move...\n" in
let () = flush stdout in
let command = input_line stdin |> int_of_string in
let i, j = (command / 3), (command mod 3) in
let board' = board_place board Cross i j in
play board' Circle
| Circle ->
let i, j = find_best_move max_depth board Circle in
let board' = board_place board Circle i j in
play board' Cross
let () = play empty_board Cross

